Cannyエッジ検出器による輪郭抽出の原理について紹介します。
2015年02月05日00:13
Cannyエッジ検出器(Canny Edge Detector)
Cannyエッジ検出器(Canny Edge Detector)は、John Cannyが考案した最適なエッジ検出のアルゴリズムです。
この手法は、従来(Sobelフィルタなど)と比べて下記の優れた特徴があります。
プログラムの処理手順は下記の通りです。
エッジの検出漏れや誤検出が少ない。(ノイズの影響を受けにくい)
各点に一本のエッジを検出する。
真にエッジの部分を検出する。
入力画像(左)とCannyアルゴリズムでエッジ抽出した結果(右)

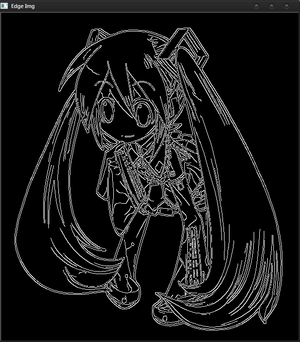
Cannyエッジ検出器の大まかな処理の流れは次の通りです。
Gaussianフィルタで画像を平滑化する。
平滑化された画像の微分を計算する。
微分した結果から勾配の大きさと方向の計算する。
Non maximum Suppression処理をする。
Hysteresis Threshold処理をする。
以降では、各処理の説明をしていきます。
1. Gaussianフィルタで画像のを平滑化
ガウシアンフィルタは、画像の平滑化処理に用いられているフィルタです。
このフィルタは、処理をかける画素の周りの画素値とガウス分布の重み付けを利用することで自然な平滑化をおこなうことができます。
入力画像を$I_{in}(x,y)$、出力画像を$I_{out}(x,y)$とすると、変換式は次のようになります。
\begin{eqnarray} I_{out}(x,y)=I_{in}(x,y)*g(x,y)\\ g(x,y)=\frac{1}{\sqrt{2\pi}\sigma}exp(\frac{x^2+y^2}{2\sigma^2}) \end{eqnarray}*は畳み込み積分を表しています。
つまり、入力画像$I_{in}(x,y)$とガウス関数$g(x,y)$の畳み込み積分を計算するだけで画像を平滑化することができます。
分散σの値が大きいほど平滑化の効果が大きくなります。
元画像(左)とフィルタをかけた画像(右)


2. 滑化された画像を微分
Gaussianフィルタで画像を平滑化した後にx方向、y方向に微分を適用します。
このフィルタは、処理をかける画素の周りの画素値とガウス分布の重み付けを利用することで自然な平滑化をおこなうことができます。
平滑化画像を$I_{out}(x,y)$、x方向、y方向に微分した画像をそれぞれ$I_{x}(x,y), I_{y}(x,y)$とすると、変換式は次のようになります。
\begin{eqnarray} I_{x}(x,y)=I_{out}(x,y)*g_x(x,y)\\ I_{y}(x,y)=I_{out}(x,y)*g_y(x,y)\\ g_x(x,y)=\frac{-x}{\sqrt{2\pi}\sigma^3}exp(\frac{x^2+y^2}{2\sigma^2})\\ g_y(x,y)=\frac{-y}{\sqrt{2\pi}\sigma^3}exp(\frac{x^2+y^2}{2\sigma^2}) \end{eqnarray}3. 微分画像の勾配の大きさと方向の計算
微分画像の勾配の大きさ$I$と方向$\theta$の計算式は次のとおりです。
\begin{eqnarray} I&=&\sqrt{I_x^2+I_y^2}\\ \theta&=&tan^{-1}\frac{I_y}{I_x}=atan2(I_y, I_x) \end{eqnarray}4. Non maximum Suppression処理
Non maximum Suppression処理により、2つの閾値で「信頼性の高いエッジ」と「信頼性の低いエッジ」を選びます。
5. Hysteresis Threshold処理
4の処理で得られた信頼性の高いエッジから、それと繋がっている信頼性の低いエッジを選んで行きます。
この処理により、エッジの検出漏れを防ぎます。
OpenCVを用いたCannyエッジ検出器を実装方法を下記の記事で紹介しています。
【Python/OpenCV】Cannyアルゴリズムでエッジ抽出する




